Robidouille - Robot Arm : Phase 1

Robot Arm : Phase 1 - In Depth

Posted 12/15/2008 by Emil Valkov
Contact:

Here is a more detailed look at the algorithm used and math involved in creating my robot arm.

RoboRealm

I use RoboRealm for vision. First, I use the RGBFilter to find my 3 blue squares. Fill, Erode and Dilate are used to smooth things out. Then finally I use the Blob Filter, to find the 3 largest blobs that are circular. The Blob Filter can set a variable (BLOBS) that contains the coordinates of the centers of gravity of my little square. I can access this variable through the RoboRealm API and move my servos in a way I'll describe in more detail below. I also use Diplay_Text, Display_Line and Display_Circle for debugging and demo purposes; I use them to overlay information on the screen. Again those modules are driven by variables that can be set though the API.

You can download the .robo file I used here.

Initialization

When I startup my program, it gets the coordinates of the 3 blue squares, but has no way of knowing which is the shoulder, elbow, or end-point. I could have used 3 different colors, but red was not an option because the plastic links I used from my Erector set were red. Also I felt the solution didn't scale well as I added more points in the future. I would need even more colors. So instead I went with all blue squares and had the robot identify its points through deep self introspection, and psycho-analysis (!). Sorry, I mean by wiggling and seeing what it does.

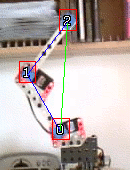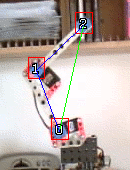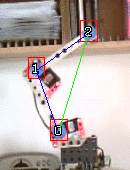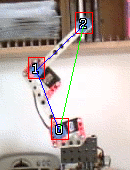
To identify those 3 blue squares, I first move the shoulder motor [0], which makes [1] and [2] move. Note that at this point I do not know which points are [0], [1], or [2].

I can determine which of the 3 points has moved the least, which identifies point [0].

You can notice point [0] moves as well even though the blue square is not moving in reality. This is due to jitter in the coordinates I receive. The phenomenon becomes more pronounced in poor light conditions, and can make the initialization fail it it's too great.

I then move the elbow motor [1], which makes only [2] move. Now the point that moves the least is [1], since [0] is already known it is excluded from the search.

Tracking the target

To track the target I make the end-point move in small increments, which allows me to work only with approximations, and converge on the target by repeating the process in a loop. Essentially, the robot makes its best guess as to how to move towards the target, and continues refining that guess on its way, until it reaches it.

I rely on the assumption the camera looks straight ahead at the arm, and not at an angle. When a single motor moves, the trajectories followed by my points, which are circular in 3D, stay circular when projected on the camera.

If I move motor [0] only, the end-point [2] will follow the green circle. A trajectory that I can approximate with its green tangent for small movements.

Similarly, if I move motor [1] only, the end-point [2] will follow the blue cicle, approximated with its blue tangent for small movements.

As long as those 2 tangents are not parallel. They form a coordinate space I can project my target onto, and extract coordinates. This coordinate space is not orthogonal as more traditional XY coordinate spaces, but it still works for us.

I can combine movement along the green and blue tangents, and move my 2 motors simultaneously to approximate the movement to the target.

Here you can see motor [0] needs to turn counter-clockwise, and motor [1] needs to turn clockwise about twice as much as motor [0].

The code was programmed in C++, which is completely overkill for this specific project given the simplicity of the algorithm. This is just the first phase though, and I assume complexity will grow in the future.

Point DiffPoint(pos1, pos2) {
	diff.X = pos1.X - pos2.X;
	diff.Y = pos1.Y - pos2.Y;
	return diff;
}

void Normalize(vect) {
	float norm = sqrt(vect.X*vect.X +
	                  vect.Y*vect.Y);
	vect.X /= norm;
	vect.X /= norm;
}

void Orthogonalize(vect) {
	float temp = vect.X;
	vect.X = vect.Y;
	vect.Y = -temp;
}

float DotProduct(vect1, vect2)
{
	return vect1.X*vect2.X +
	       vect1.Y*vect2.Y;
}

float Determinant(vect1, vect2)
{
	return vect1.X*vect2.Y -
	       vect1.Y*vect2.X;
}

xAxis = DiffPoint(points[2], points[0]);
Orthogonalize(xAxis);
Normalize(xAxis);

yAxis = DiffPoint(points[2], points[1]);
Orthogonalize(yAxis)
Normalize(yAxis);

vect = DiffPoint(target, points[2]);

float cosXY = DotProduct(xAxis, yAxis);
float cosXV = DotProduct(xAxis, vect);
float cosYV = DotProduct(yAxis, vect);

float sinXY = Determinant(xAxis, yAxis);
float sinXV = Determinant(xAxis, vect);
float sinYV = Determinant(yAxis, vect);

result.X = cosXV - sinXV*(cosXY/sinXY);
result.Y = cosYV + sinYV*(cosXY/sinXY);

Here is pseudo-code that describes what the program does.

I start with points[3], which is a 3 item array containing the 2D positions of the shoulder[0], elbow[1], and end-point[2].

From there I generate the 2 axis, by getting the radius of a circle, getting its orthogonal vector, and normalizing it.

Then finally I project my target on the xAxis parallel to the yAxis to get one coordinate. And on the yAxis parallel to the xAxis to get the other. You'll note that vect is not normalized on purpose, this allows my result to be proportional to vect's length, and so make smaller movements as a get closer to the target.

The dot product is used to determine cosines, and the cross product is used to determine sines, by calculating determinants.

Final Comments

I hope this answers most remaining questions. I tried not to make it too dry.

If we place the camera at an angle, the circles in 3D, will be projected as ellipses as seen by the camera, and the method presented here no longer works as is. And of course if we add an extra degree of freedom to this arm, the movement of the end-point will no longer be constrained to a plane. So to continue working, we need to solve the general problem, with the camera at an angle. Adding an extra camera and using stereo vision to triangulate coordinates of our points in 3D seems the natural choice for the next step.